Introduction
Given enough fuel assistance, how far can a Commander travel in Supercruise?

This will be far from the first time such a question has been considered. However, occasionally we also encounter the notion that there is somehow a limit on the possible distance. With enough supporting vessels, there is no limit, and there are also several different recipes—enough to inspire a full article piece about it—which a large enough group of Commanders can use to surpass any arbitrary distance target.
The types of calculation used here are millennia old, dating far back to Earth¹ prior to any form of flight, although the modern application of them is quite pleasing. We hope that this converts the thought-provoking claim above into arguments simple enough for most readers to understand and use in future oneself.
1. As a caution for those interested in human history, there is no longer anything to be gained by visiting Earth unless you intend to study old ruins. An interstellar tour of Imperial space will provide a far greater overview of Earth's legacy than any attempt to visit the planet itself would achieve.
Convention
The direct, quantifiable answer to the more simple case with one Commander is actually just a matter of testing to find the starship which can spend the most time in Supercruise, coupled with an understanding of Frame Shift Drive acceleration in the presence of a gravitational field so that we can convert time to distance. We will test both of these and present the results towards the end, but for the moment this is a secondary distraction from investigating how to achieve an unlimited journey.
Instead, waive any concern regarding the actual distance numbers by introducing new units of mass and time, defined to be the maxima of each afforded by a single vessel:
- However large the fuel tonnage may be, use 1 to represent that mass.
- Whatever time that can afford in Supercruise, use 1 to represent that duration.
Excepting the transfer overhead and perhaps reserving a little fuel to escape via hyperspace jump, this single unit can then be used interchangeably between mass and duration, and any supporting contributions can be accounted as fractional¹ parts of that original whole. Depending on the starship, you may think of this as being "one Imperial Cutter" or "one Type-9 Heavy", to name a couple of obvious choices. We will call it one leg of a total we call the journey.
Either way, it refers to one full load of fuel and/or one measure of the Supercruise time that load affords. Regardless of support scheme, one vessel with one full load of fuel is able to travel for one unit of time.
1. Working with integer fractions is something which comes very naturally to Imperial folk. We prefer to leave quantities in terms of a fraction or ratio wherever possible, as you will soon discover if not already familiar. This should present no problem if you are comfortable with the sum of a half and a third becoming five-sixths (for example).
Mistakes
Incorrect assessments of the maximum achievable journey usually make one of these basic errors:
- Assuming that a valid support scheme is the only possible method.
- Assuming that the journey achieved by a support scheme cannot be improved.
The scheme presented in this section fails to achieve an unlimited journey, but it provides a great starting point for understanding what comes after it.
Investigation
To begin with a genuinely useful observation, suppose we have two vessels. If both travel together for a half-leg, the secondary vessel could then refuel the primary, ready to complete an additional full leg atop the half already travelled.
This is a great starting point for any support scheme, and is actually the best start possible. It is equivalent to linking the fuel tanks such that the pair burns secondary fuel at double the rate, then discarding the secondary tank once empty. Nothing can prevent the fact that it costs double to keep both tanks moving, yet there is nothing to be gained by discarding the secondary before it is depleted.
This idea goes awry when introducing a third vessel without respecting the order of operations:
- All three vessels travel a half-leg, then one refills the primary and leaves.
We now have a full primary, and a secondary with half. - Both vessels travel a quarter-leg, then the secondary refills the primary and leaves.
Of course, if we introduce a fourth vessel being present for the above, it would have quarter fuel remaining and therefore would support an additional eighth-leg. In general, each additional vessel extends the journey J by half that of the previous vessel:
J = 1 +
Intuitively, it is quite clear that this geometric series drifts ever-closer to the value 2:
Despite the impossibility of performing an infinite summation directly, this intuition is not fallacious. We can provide some assurance of this by formalising it a bit in terms of the finite:
- A finite amount of terms will never breach 2, so the total cannot be something higher.
- Some finite amount of terms will always breach a number arbitrarily close to 2, so the total cannot be lower.
Calling J equal to 2 is still a fragile notion which requires an imaginative leap, however we can at least be sure that if a finite total for that series exists then 2 is the only possibility.
By this point, any experienced Commander surely will imagine a starport approach in Supercruise; the balance between closure and deceleration where the remaining travel time appears to freeze, continuing to make forward progress at a diminishing rate.
Analysing this footage, we can see that the remaining distance is halved every ~4.25 seconds, actually slightly less¹. Were this to continue, we would be cruising forever in progressively worthless 4.25-second intervals, while also never overshooting the target. In practice this pattern is disrupted by factors such as Destination Lock or a 30 km/s minimum speed, but otherwise captures perfectly the concept of an infinite summation having a finite result.
1. We performed a cursory check for any suspicious exactness in the Supercruise decay rate, and found that 2-1 in slightly under 4.25 seconds could match π-1 in 7 seconds exactly. Given that gravitational effects can be modelled as a spherical surface area 4πr2 which becomes less dense as the radius r increases, it should be no surprise that a division by π appears, at which point this 7 seconds looks much like a deliberate specification choice. To this day, the original Frame Shift Drive design process remains a trade secret of Sirius Corporation, so any consequences of such a choice are now baked into the FSD schematics.
Justification
Suppose we have an endless supply of vessels, but that the total for J is a finite value we can treat arithmetically. We can use a little sleight-of-hand to produce a larger series by doubling J:
J = 1 +
2J = 2 + 1 +
Once doubled, it is as if each term has become the term to its left, generating a spare 2 term at the start.
Ordinarily this would leave us with a gap at the end of the series, but in this case there is no end, because our original supposition was that the supply was endless.
That specific property is the reason that we are able to obtain a fresh
It is no coincidence that we have aligned the two series summations above, making it easy to see that they both have the same infinite tail of terms. Subtracting the original series from the doubled series will cancel out the infinite tail, leaving only that spare 2 term:
2J − J = 2
The left side is simply J itself, yielding J = 2.
Again, if such arithmetic upon J is assumed to be valid in the same context as a finite quantity, we can only conclude that J has the value 2. To state it another way, we have shown that doubling J has the same effect as increasing it by 2, a unique behavioural property for which the only matching value is 2.
Despite all of these indications that we have a valid result, for many people this can still feel wrong¹, as if we are really just assigning a value as opposed to proving it definitively. We understand you there, and you are absolutely correct; this only holds together because the series is gracious enough to be convergent to a particular value. The same style of argument can be misused to assign spurious values to summations which do not converge, and we will reveal how that happens in Appendix A, along with how it can be used somewhat legitimately. In the meantime, please be assured that any contradictory results obtained this way will be denied and the series declared to be divergent.²
In any case—however enticing this result may be, do not become too convinced by its elegant-looking journey limit of exactly two. A moment of thought should tell you that this is a terrible scheme, for much time is spent keeping several vessels online with very little actual fuel held. It can be improved, and dismissing vessels before that situation occurs is the way to do it.
1. Always trust your feelings. If something works mathematically but still feels wrong, it is because there is a better fundamental way to understand it, or even a deep connection to be discovered. It can help to pause and review exactly what the symbols represent, perhaps devise some new notation to clarify the matter, enabling us to make useful statements more comfortably. In this case, the problem is that the symbol J is used for both an infinite summation and a single value. More about that later.
2. "Divergent" can mean either escaping to infinity or oscillating around without settling, which is actually still a meaningful distinction. If a series contradicts basic arithmetic but is at least well-behaved enough to move only in one direction, you know you are dealing with something infinite in nature.
Rectification
As suggested earlier, the faulty method above is only limited in its potential due to the order of operations. Despite being an earlier term in the summation, the half-leg need not and should not be placed that early in the journey.
However, before proceeding to correct the real underlying problem with that method, it is very much worth noting that just a little more thought would repair it into being one which actually does give an unlimited journey, albeit inefficiently.
Let every vessel travel half as before. Then, rather than just one vessel resupplying the primary, half of the vessels could each choose a partner and do the same thing. This exodus leaves us with a halved fleet which has travelled one half-leg, but all remaining vessels have full fuel again.
This process can be repeated, where each halving of the fleet gives us an additional half-leg for the journey. This is indeed a recipe for an unlimited journey; we can exceed any target by starting with one leg then adding on any number of half-legs needed just by doubling the number of vessels that many times.
More formally, if n ≥ 0 is the number of resupply events then 2n vessels yield a journey of 1 +
Clearly, dismissing more vessels at each stage—particularly with greater numbers of vessels dismissed at earlier stages—is giving us such a dramatic reduction in travel expenses that it is enough to upgrade the journey from finite to infinite. This, as opposed to the flawed prototype above, is what we shall call the halving method.
Optimisation
We can improve upon the halving method by observing that we are still paying fuel to haul around quite a lot of empty space. At the moment just before the exodus, we have an array of half-empty tanks which surely could have been replenished in a smaller increment at an earlier point, thus avoiding having to fund a half-leg for every vessel each time.
To see what we can do, return again to the conceptual idea of linking the fuel tanks such that all expenditure is taken from one vessel. This is unphysical directly of course, however it does yield distances we can use. The distance travelled by a theoretical fleet for which all fuel is drawn from one vessel will match the distance after which a real fleet should stop and redistribute.
The two-vessel case remains the same as before, but consider the three-vessel case.
To fund the fleet, our contributing vessel is spending fuel at triple rate, so its contribution moves the fleet by a third before it parts and leaves us with the two-vessel case.
In general, n vessels can fly
With that in mind, try using those distances as a template to dismiss a vessel as soon as its remaining fuel would replenish the others:
- As before, two vessels would travel half then refuel the primary to give it an extra full leg.
- With three vessels, the fleet can travel one-third before the remaining two-thirds in a vessel would refuel the other two. That duo can then proceed as with the two-vessel case.
- With four vessels, the fleet can travel one-quarter before the remaining three-quarters in a vessel would refuel the other three. That trio can then proceed as with the three-vessel case.
- In general, n fully-fuelled vessels can travel
1 /n ( to the n−1 others.n−1 )/n
Again, accepting that the summation order is the reverse of the chronological order, our journey J now becomes:
J = 1 +
This sum is the harmonic series, and grows infinitely without limit despite each term being smaller than the last. This counter-intuitive fact is almost two thousand years old, and our stubborn disagreement over how best to prove it will be the basis for presenting two different arguments.
Odd/even proof by contradiction
Suppose the harmonic series H is actually finite, such that it can be treated arithmetically. Then, separate its terms into sums of odd and even unit fractions:
H =
The sum of even fractions is just the same as H itself with all terms halved:
H =
The odd fractions are larger than the corresponding even fractions, yielding the obvious contradiction of H being equal to something larger than itself, and therefore not a finite quantity as supposed. Simple, is it not?
V wants me to be clear about that claim, so continue with splitting the odd harmonic series into an even series plus a series of the differences¹:
H =
Replace that second sum of even fractions similarly, then subtract H from each side:
H =
0 =
This is clearly impossible. By that contradiction, H must be an infinite value to which standard arithmetic does not apply, and I will leave you and V to proceed with over-thinking it all.
1.
Challenge: Find the value of
This is not trivial; it requires a bit of creativity and good working knowledge of calculus, which is both a caution and a hint. It is also beyond scope compared to everything else here, earning itself a place in Appendix B.
Grouping proof by comparison
Now that Aleksandra is done swindling you with dubious arithmetic, a much more relatable and quantifiable means is to collect the terms of the harmonic series into successive groups which double in size, then choose a comparison series C which is designed to be smaller:
| n : | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | ... |
| Hn : | 1 | ... | |||||||
| Cn : | ... |
Here, each term in C is just the largest power of a half which is less than the corresponding term in H.
Stated formally, Cn =
Note that:
C =
Collect each group of terms, then simplify the fractions:
C =
C =
Therefore, grouping the terms of C shows us that it is infinite, because we can exceed any target value by contriving ever more halves. Then, because C was designed such that H is superior to C term-for-term, H must also be infinite.
Regardless of means of proof, it is clear that H represents an infinite journey we can call the harmonic method. Together with the halving method, these are nice results; unfortunately, they will not actually work.
Limpets
In practice, no additional vessels will be of any use to the primary Commander if all they have is a hold full of fuel with no limpets to transfer it, and synthesis is hardly capable of supporting the volume of transfer we will require. The above schemes will not be able to replenish nearly as much fuel when it costs equal cargo space for fuel transferred, and this raises some alarming questions:
- What scheme can we use?
- Does this then limit us to a finite journey?
Thankfully, we can show that the journey is still unlimited even with the overhead of carrying limpets. More so than that, there are actually multiple adaptations possible, and together they expand the scope for trade-off between simplicity and efficiency even further.
Reinforcement methods
Once again, with very little extra thought, there is an inefficient but simple way to adapt any previous method so that it works with the limpet requirement.
Given that fuel spent on transfer now costs double capacity but the fuel spent on movement has not changed, we should be able to fix any method just by adding more support vessels at each stage. Support teams will always be able to travel together, giving us a reinforced version of said method.
Halving method
The reinforced halving method becomes somewhat of a misnomer, where each stage now divides the fleet by three. We can use teams of three vessels to fly a half-leg, two of which have a quarter each of their capacity devoted to limpets. These two then replenish the other with their remaining one-quarter capacity of fuel each.
Three teams of three vessels, nine in total, can then perform this process twice. If two of those team leaders themselves carry a quarter load of limpets, they can band together after one iteration to form a new team.
In general, the journey now requires 3n vessels to achieve, but is still represented by the expression 1 +
Harmonic method
The reinforced harmonic method is a bit more difficult to manage, but grows in scope more sanely. First, re-label the primary vessel as being in Group A (alone; a group of unit size). The purpose here is to consider the harmonic series in terms of a group of vessels supplying each element.
Group B is exactly as we had in the reinforced halving method; two vessels which travel along for a half-leg then supply the single vessel in Group A with a quarter fuel each.
After travelling for one-third, the three vessels in Groups A and B will each require one-third fuel, total three-thirds. Group C vessels will have two-thirds capacity remaining, meaning that each can give one-third fuel, so we will need three vessels in Group C. This also introduces some extent of coordination, with Commanders in Group C each choosing one vessel to resupply.
For Group D, we have six vessels in Groups A-C which will each need one-quarter fuel, total six-quarters. Each supply vessel will have three-quarters capacity to spare—at which point we realise that a halving will imply working in eighths instead. We need twelve-eighths fuel, and each vessel can supply three-eighths, so we need four vessels in Group D. Coordinate by splitting everyone into teams of three consumers and two providers, then providers measure out one-eighth to each consumer in their team.
The pattern should become clear:
- Ten vessels in Groups A-D each need one-fifth (total ten fifths), where five vessels in Group E spend one-fifth then supply two-fifths each.
- 15 vessels in Groups A-E each need
1 /6 2 /12 30 /12 2 /12 5 /12 n(n−1) /2 1 /n ( . In group n, n vessels spendn−1 )/2 1 /n ( each.n−1 )/2n
Reinforcement is great in how quickly it revives our ability to travel infinitely, but we could still use some more efficient ideas which are designed from the start with limpets in mind.
Native methods
Short halving method
The original idea returns to make one more contribution. Rather than insisting that our fleet moves in half-legs and using 3n vessels to fund that luxury, just return to using 2n vessels and reduce the travel distance at each stage.
To deduce how far this distance is, suppose once again that we have two vessels with linked fuel tanks. The primary vessel now costs double to draw from the secondary tank, which means it costs a total of triple to keep those two vessels moving, so our distance increment must be a third.
Changing this back into a physical context, two vessels can travel one-third before the secondary uses the remaining two-thirds capacity to send one-third fuel to the primary. This arrangement scales up just as before, but each halving of the fleet now adds one-third to the journey.
Thus, the short halving method has us use 2n vessels to yield a journey of 1 +
Odd harmonic method
To avoid requiring that a specific number of vessels are added at each stage, we can restore instead the more elegant approach which scales much more inclusively to any number of vessels, and also offers the best distance gain for each vessel involved.
Rather than attempting to construct a method which fits a harmonic sum specifically, just do as we did before the harmonic pattern emerged in the first place; add one vessel at a time, and discover how much additional journey is gained.
At each stage, the journey will be extended such that half of a vessel's remaining capacity will refill all previous vessels:
- As we know, vessel B adds an extra third, then uses the remaining two-thirds capacity to give one-third to vessel A.
- Vessel C adds an extra fifth, then uses the remaining four-fifths capacity to give two-fifths to the other two vessels, one-fifth each.
- Vessel D adds
1 /7 6 /7 3 /7 1 /7 - Vessel n adds
1 /(2n−1 )( to give2n−2 )/(2n−1 )( to the other n−1 vessels,n−1 )/2n−1 1 /(2n−1 )
Of course, this gives us a different summation for the length of journey J:
J = 1 +
For the odd harmonic method to succeed, that new summation must also be shown to grow infinitely. This it does, and we actually devised several different ways to show it. For a bit of fun, we decided to start by adapting each other's approach to the harmonic series from earlier.
Term comparison
I do not normally advocate scaling and shifting an infinite series around when a less abstract means will suffice, but I will admit that Aleksandra has left me with very little additional work to do. The previous proof by contradiction already contains the needed solution in its intermediate stages.
Recall that the odd unit fractions are larger than the evens:
1 +
As before, the even fractions are just half of the harmonic series H:
1 +
This time around, we already know that H grows infinitely, and halving its terms has no effect on that basic fact¹. Enough terms of H can already beat any arbitrarily high target, and halving the terms is equivalent merely to doubling the target.
With Jn >
1. This was the crux of the contradiction argument; the entire point was to discover that arithmetic upon H is meaningless.
Grouping multiplicatively
I have agreed to this on the condition that V allows me to adapt the tabulated presentation from earlier. Replace our journey J and halve the comparison series C:
| n : | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | ... |
| Jn : | 1 | ... | |||||||
| Cn : | ... |
C consists of an infinite supply of quarters, so J is infinite because Jn > Cn.
Grouping additively
We did find a pleasing medium between those two proofs. It relies upon a comparison to the harmonic series without venturing further into abstract manipulation, and also makes use of grouped terms without being quite so uneconomic in contriving an inequality. It is also a bit more lengthy, so it has been moved to Appendix C.
As an exercise for the numerically inclined, try grouping the odd harmonic series this way:
1 +
Then, ask yourself:
- What happens when comparing those groups to the harmonic series?
- Is there some way to make said comparison more manageable?
- Will that observation always be the case? Prove it if so, or fix it if not.
As stated above, there is a complete description in Appendix C, but if you have any appetite for this type of solution discovery then please consider those hints and attempt it first yourself.
Method comparison
Now that we have a good selection of different means we can use to organise a journey, here is a concise view of how they perform:
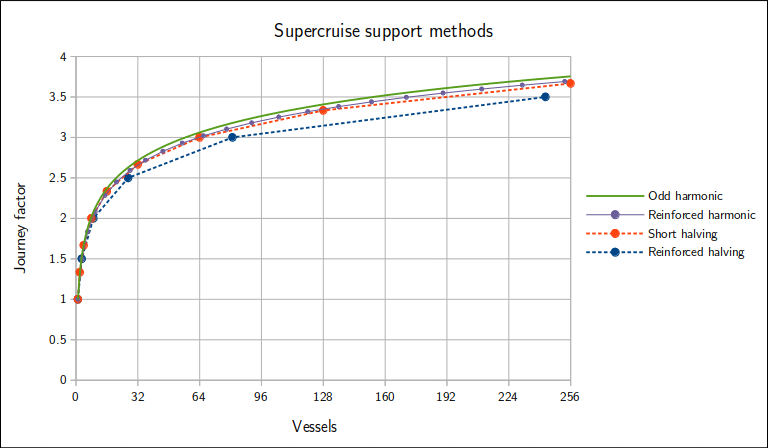
The odd harmonic method is quite predictably ahead of anything else, although in practice there is also no limit on how difficult it becomes to perform, so other methods still have a purpose for very large fleets. When your fleet is some multiple of an obscure but manageable group size such as 11, the odd harmonic method will shine.
Unless you need a fast scheme to handle a massive fleet size which just happens to be an exact power of 3, we suggest scrapping the reinforced halving method. Conversely, a massive fleet which hits a power of 2—or even simply contains a large power of 2 as a factor—would be very well-served with a few rounds of the short halving method.
The reinforced harmonic method does not perform all that differently to short halving, so we suggest only using this if your fleet size matches (or is a multiple of) one of the numbers in its sequence of
Hardware
Before we close with a few practical points for how to design a full journey, it will help a lot to introduce some context for that by understanding first what starship and modules will be best to use.
Goals
The following starship properties are desirable:
- Large total fuel/cargo capacity.
This is the most important property, to which the total Supercruise time is directly proportional. - Low power draw during Supercruise.
To an extent, we can improve our Supercruise time per fuel by using small, low-rating modules. - Varied classes of optional modules.
The support vessels need this to help achieve arbitrary fuel/cargo ratios.
For direct capacity, clearly we will need the likes of the Type-9 Heavy at 854 fuel or Imperial Cutter at 858 fuel.
Given that the Thrusters module is the largest consumer of power, starships with low hull mass will have the advantage, because a weaker Thrusters module imposes a lower maximum total mass. This certainly favours the Type-9 Heavy at 850 T hull compared to the Imperial Cutter at 1100 T. The Anaconda at 400 T also caught our attention, however this will not be worth the capacity drop to 502 fuel. Several other starships have similarly good capacity to hull mass ratios¹, though none come anywhere close to having over 800 raw capacity.
The Type-9 Heavy also has a very well-balanced module class distribution, while the Imperial Cutter uses modules which are fewer but larger. At this point, the Type-9 Heavy will become the definitive choice if its power draw can be made low enough to overcome the minor fuel deficit.
1.
We wish to commend Zorgon Peterson for the Hauler, which is spectacularly lighter than anything else when indexed against its capacity, being able to carry 2.14 times its mass in fuel (actually
Fuel consumption
With plenty of data courtesy of Gutamaya, plus some secondary experimentation of our own, we know the following:
- The fuel cost of maintaining module power is 0.08 T/MWh.
- Maintaining Supercruise costs an additional 0.72 T/h, equivalent to supporting an extra 9 MW.
Given the total Fuel T and the used Power MW, this yields the following expression for total Supercruise time:
Time =
We will use this to evaluate the base performance of different starships. As a standard for comparison, this is done always with only the Thrusters, Frame Shift Drive and Life Support enabled, as will be the case during Supercruise. Resupply stops need Life Support, Sensors and Fuel Transfer once in position, however we will regard these pauses as negligible for the sake of comparison.
Given that Thrusters will be addressed separately, the brief guide to low-draw module choices is the following:
- The Power Distributor is always disabled, so it can be 1D.
- The Power Plant is mostly inconsequential, so 2D will be fine unless the 2A power output is needed.
- Sensors, Life Support and Fuel Transfer can be E-rated, unless D-rated would lower the Thrusters requirement.
- The FSD can be 2E unless you require a return jump, noting that this choice impacts Supercruise time.
As a general instruction for pilots, the Life Support is always enabled, and the Power Distributor and Cargo Scoop are always disabled.
The mass game
As noted above, the largest benefit to Supercruise time is through using Thrusters with lower power draw. The effect is significant enough that it becomes worth making an effort to reduce mass if doing so enables the use of smaller Thrusters, even if it involves D-rated modules elsewhere with slightly higher power draw. Optimising the journey is almost entirely a matter of finding the weakest possible Thrusters which can still support the starship mass.
For engineering, the biggest difference is with Drive Distributors, which will raise the maximum mass supported by the Thrusters. Start with a basic grade of Reinforced engineering for this; the slight increase to module mass is superficial compared to Dirty increasing the power draw and Clean reducing the supported starship mass. After that, check whether a decent Lightweight grade for Sensors and Life Support will cross a threshold for using smaller Thrusters.
Here are the relevant Thrusters thresholds for maximum starship mass. Only the D- or E-rated Thrusters matter here; this is because higher-rated models draw more power than using E-rated models of the class above.
| Thrusters | Stock | Engineered |
| 4E | 420 | 462 |
| 4D | 473 | 520 |
| 5E | 840 | 924 |
| 5D | 945 | 1040 |
| 6E | 1440 | 1584 |
| 6D | 1620 | 1782 |
| 7E | 2160 | 2376 |
| 7D | 2430 | 2673 |
| 8E | 3360 | 3696 |
| 8D | 3780 | 4158 |
Recalling the starship numbers from earlier:
- A Type-9 Heavy hull plus fuel is 1704 T, enabling engineered 6D Thrusters.
Even without Lightweight modules, the starship can fit within the 1782 T threshold. - An Imperial Cutter is 1958 T, forcing 7E Thrusters.
D-rated modules can keep this under 2160 T without any engineering, while 2376 T becomes easy regardless. - An Anaconda is 902 T, narrowly enabling engineered 5E Thrusters.
This is only barely achievable¹ with full top-grade Lightweight and Stripped Down D-rated modules.
Any effort less than that will bump the specification up to 5D Thrusters.
This completes the starship design considerations, should you wish to follow a similar process. We will now see how our examples translate into Supercruise time.
1. This also bends the previous rules slightly by allowing that a class 4 Fuel Tank will be replaced with a 3D Fuel Transfer—itself top-grade Lightweight, of course. We were unsure at first whether the final results comparison should incorporate Fuel Transfer, but the Anaconda achievement was pleasing enough to go with "yes". Moreover, there is a decent case for preferring that the actual numbers involved are more representative.
Performance
To reiterate our comparison conditions:
- All starship builds have one class 3 Fuel Transfer.
- All other optional modules are treated as fuel.
- The core Fuel Tank module is included in the capacity total.
- Power draw in Supercruise is minimised via small modules and any necessary engineering.
- Only the Thrusters, Frame Shift Drive and Life Support modules are active.
- Supercruise is active.
Possible deviations aside, this should give us a sensible base amount of Supercruise time. For example, we are aware that a class 1 Fuel Transfer costs less fuel per active limpet to install, but this is not without its trade-offs. We are also aware that the primary vessel in the fleet needs no Fuel Transfer at all, however this is a superficial point which does not affect the majority of the journey, and it distracts from a even and realistic comparison.
Adhering to the above, the top five starship configurations we could achieve¹ are the following:
| Starship | Fuel T | Power MW | Time h |
| Type-9 Heavy | 846 | 6.40 | 686.688 |
| Imperial Cutter | 850 | 6.96 | 665.727 |
| Federal Corvette | 642 | 6.40 | 521.104 |
| Anaconda | 486 | 4.90 | 437.050 |
| Type-7 Transporter | 334 | 4.74 | 303.857 |
We can see that the slightly lower capacity of the Type-9 Heavy is more than offset by the reduced power draw. If anything, the Imperial Cutter is an undeservedly close competitor given that its only real advantage here is in carrying 4 T more fuel, an increase of less than 0.5%.
1. The presented loadouts have the minimal engineering required, where that has priority over power draw concessions. Most could be made lighter, but not enough to make any further difference.
Practicality
Despite the odd harmonic method being about the best we can do theoretically, any pilot who owns more than a stock starship will notice that the required fractions become unmanageable quite quickly.
Heavy starships achieve high cargo/fuel capacity by means of large, indivisible bulk modules, so you would be quite correct to question whether it is actually practical to achieve a cargo fraction such as
Conveniently, if we fit a Type-9 Heavy with Fuel Transfers of classes 3 and 1 (like this), it is actually possible to achieve those fractions each with a sensible spare fuel budget remaining. A little excess is advisable here, so that we are covered for keeping modules online during the time spent transferring fuel.
The following table describes how to assemble a team of those Type-9 Heavy vessels with different cargo ratios so that they can perform the odd harmonic method:
| Vsl. | Leg | Ratio | Tanks | Racks | Travel | Spare | Time |
| 2 | 8 7 6 5 4 2 | 8 4 3 | 280 | 4 | 227h 16m | ||
| 3 | 8 7 5 4 3 2 | 8 6 4 | 168 | 4 | 136h 22m | ||
| 4 | 8 7 5 2 | 8 6 4 4 3 | 120 | 4 | 97h 24m | ||
| 5 | 8 7 4 3 | 8 6 5 4 2 | 93 | 7 | 75h 29m | ||
| 6 | 8 7 4 | 8 6 5 4 3 2 | 76 | 8 | 61h 41m | ||
| 7 | 8 7 3 | 8 6 5 4 4 2 | 64 | 4 | 51h 57m | ||
| 8 | 8 7 2 | 8 6 5 4 4 3 | 56 | 4 | 45h 27m | ||
| 9 | 8 7 | 8 6 5 4 4 3 2 | 49 | 3 | 39h 46m | ||
| 10 | 8 7 | 8 6 5 4 4 3 2 | 44 | 8 | 35h 43m | ||
| 11 | 8 6 5 4 3 2 | 8 7 4 | 40 | 4 | 32h 28m |
Anyone attempting a journey of this type should also observe that the support methods can be nested to produce a combination method. For example:
- 12 vessels could do odd harmonic in groups of 3, followed by two rounds of short halving.
- 16 vessels could do odd harmonic in groups of 4, followed by odd harmonic again with the final 4.
This extent of customisation is incredibly valuable, allowing a journey director to trade between efficiency and practicality. Always begin by determining how many vessels you have and to what extent you will be able to achieve the required fractions, then design your journey accordingly.
When combining methods that way, you will find that the best fleet sizes are those which are highly divisible, such as 18 or 24. Such numbers can be constructed by multiplying together a lot of small prime factors such as 2s and 3s, while avoiding larger prime factors such as 13 or 17.
Always check the prime factors before committing to a particular fleet size. Regardless of the method choices, each supply round must divide your fleet down by some of those prime factors. This means that any tricky factors in the list are inevitable and unavoidable; if they appear, a method which handles that group size will have to become part of the journey.
If you find yourself in that situation, probably the best you can do is to design a custom split between suppliers and consumers.
For example, a group of 13 could fly with 6 resupplying the other 7.
It costs 6 + 2 × 7 = 20 to run that fleet, so the leg will be
In general, use the following design process:
- Choose a supplier/consumer split.
Fewer suppliers will be more efficient, but will incur higher spare capacity more often. - Cost = Suppliers + 2 × Consumers.
This denominator is the total capacity needed to move the fleet by 1 unit of fuel. - Units =
Capacity /Cost
This is the number of travel units provided by one supplier vessel. Critically, the remainder is how much spare capacity you will have, which ideally would be a small amount of fuel but can also be used as an error margin for meeting the cargo demand. - Travel = Suppliers × Units.
Very important number; instruct your pilots to spend exactly this amount of fuel on flight. - Cargo = Consumers × Units.
This is your cargo target to be met by adjusting the module allocation, and will be the number of limpets sent by each supplier vessel. You can not overshoot by more than the available remainder, and please note that overshooting at all will be at the expense of holding spare fuel.
That initial choice provides a very welcome degree of freedom, which should be used to trade between efficiency, a sensible remainder, and an achievable cargo target. For what it is worth, the coverage of group sizes up to 11 in the table above should suffice for most purposes.
Result
As promised much earlier, we will estimate what extent of distance can be achieved this way. Truth be told, we were actually far more interested in this application from a purely theoretical perspective as opposed to how a final number turns out, but we also refuse to disappoint by stopping short of that.
For the vast majority of such a journey, the fleet will be travelling at the maximum Supercruise speed of 2001c, such that simply multiplying this by the journey time should provide a fairly accurate distance. We can identify the following detractions:
- Each resupply will incur a little overhead, although this is well-answered by each vessel configuration above also having a few units of extra fuel. With 3 active limpets the longest resupplies will take around 70 minutes, however each spare fuel provides over 580 minutes for this purpose, so we will consider this to be negligible.
- Accelerating back to 2001c after a resupply will take a bit of time. It will be far quicker than when escaping the gravitational field of a star, but it will also be consuming fuel at the full Supercruise rate. The healthy amount of excess fuel from the resupply budget will have to cover this.
- Initial acceleration to 2001c does take noticeable time to escape the star, actually just under 57 minutes. The distance covered during this phase is 0.16 Ly, where open space at 2001c would have covered 0.217 Ly, so our final results will be 0.057 Ly below our raw totals.
With that in mind, here are the distances achieved by the odd harmonic method:
| Vessels | Leg Ly | Total Ly | Final Ly |
| 1 | 156.378 | 156.378 | 156.322 |
| 2 | 51.879 | 208.258 | 208.201 |
| 3 | 31.127 | 239.385 | 239.328 |
| 4 | 22.234 | 261.619 | 261.562 |
| 5 | 17.231 | 278.850 | 278.793 |
| 6 | 14.081 | 292.932 | 292.875 |
| 7 | 11.858 | 304.790 | 304.733 |
| 8 | 10.376 | 315.166 | 315.109 |
| 9 | 9.079 | 324.245 | 324.188 |
| 10 | 8.152 | 332.397 | 332.340 |
| 11 | 7.411 | 339.809 | 339.752 |
Interesting, is it not?
● ● ●
Appendix A
To see how a value can end up being assigned to a divergent sum, consider the following series S, chosen to be deliberately profound:
S = 1 + 4 + 42 + 43 + ...
S is very clearly infinite; its terms only get larger very rapidly, each being a factor of 4 above the last, such that enough terms can surpass any arbitrarily high value.
It looks as if we might be able to multiply S by 4 and subtract that from S itself, but surely something must fail if we suppose that S can be treated arithmetically that way:
4 S = 4 + 42 + 43 + ...
S − 4 S = 1
S = −
As expected, this is clearly impossible; a summation involving only positive integers can become neither negative nor fractional. Either of those contradictions are enough to disprove the supposition that S has a finite value, and therefore we may conclude that S is infinite.
That said, something should feel suspicious here, as if there is more to discover than simply declaring S infinite and leaving it at that. The equations just yielded a value for S quite easily, which should prompt a few questions:
- Is there some structural aspect of the 4n numbers which is captured by the value −
1 /3 - Can we state that if S had to be represented by a value, the correct value would be −
1 /3
The answer to those questions is "In a sense, yes", and this should not require much more thought than with the first infinite series in this article.
We have an object for which multiplying by 4 has the same effect as subtracting 1, a property which is indeed associated with (or characteristic of) behaving like the value −
Most GalNet material refers to this as the assigned value, which we view as a miserable effort to avoid the word equal, nothing but a euphemism. The words associated value or characteristic value are a little better, but really we need something which connotes "the value remaining upon cancellation of the infinite tail".
To see this by example, suppose you needed to find the finite value M such that:
M = 45 + 46 + ... + 415
Of course, you could just start multiplying and adding, but obtaining an eventual result that way is not the purpose of the example. Instead, note that the same method by which we determined a value for S—again, assuming that S can be treated that way—could also be used to select a sub-series of S which equals M:
45 S = 45 + 46 + ... + 415 + 416 + 417 + ...
416 S = 416 + 417 + ...
Subtract to cancel the infinite tail of terms:
(45 − 416) S = 45 + 46 + ... + 415
This sub-series extracted from S matches the value M we require. Curiously, despite M being explicitly finite, we now have an expression for it which somehow contains S. The only way this can be at all meaningful is if that associated finite value for S determined via cancellation—its finite remainder, if you will—can be used here:
M = −
Following that arithmetic gives us 1431655424 exactly, the same as if we had performed the full summation.
This is one of the most fascinating mathematical quirks one can encounter, especially considering how relatively easy it is to demonstrate. Alone, S is obviously infinite, and it is still obviously wrong to claim that it is equal to some negative fraction. However, when our specific use of S involves cancelling out its infinite tail, the self-destruction leaves behind that quantity as a scale factor. Moreover, we actually need it there for our result to be correct.
Think about it—we were only able to obtain that negative third originally because we performed an initial test upon S to discover its finite remainder. We achieved this by subtracting 4S from S, an operation which cancelled the infinite tail, thus forging the result within the realm of the finite where it is allowed to exist. If anything, the only problem here is how the symbol S remains the same before and after the cancellation, referring both to the infinite series and to the finite remainder.
If that is simply how it works then there is no fundamental paradox; all we need to do is label S appropriately. We could call the infinite series version S∞ and rewrite our original formulation like this:
S∞ = 1 + 4 + 42 + 43 + ...
4 S∞ = 4 + 42 + 43 + ...
S∞ − 4 S∞ = 1
(1 − 4) S = 1
S = −
See the difference? Tracking the disappearance of the infinite tail allows us to be clear about whether we are referring to an infinite series S∞ or to its finite remainder S. Term-shifting is allowed upon the former, while the latter may appear in an expression for calculating a finite quantity.
We wish to congratulate any readers who noticed that the divergent sum confusion could be bypassed, at least in this case, by discarding S∞ and replacing it with powers of a quarter:
S∞ = 1 +
M = 415 S∞ − 44 S∞ = (415 − 44) S =
That would have ruined the revelation, though. Also, the resulting S∞ versus S notation seems like a most welcome clarification even for the case of that convergent sum, don't you think?
As we leave this topic, please observe that the above notation is a product of INIV, not of Galactic consensus. We do not wish to mislead, yet we also found existing GalNet material to be unacceptably deficient in showing what it means for something with an infinite limit to have an associated finite value, hence presenting our own understanding of it. If you wish to research it further yourself then seek out divergent series and analytic continuation, but please retain our notion of a finite remainder as a shield against confusing a series with a finite expression result, and reject any sensationalist nonsense which claims the two are somehow equal.
Appendix B
Brave, are we?
Please be aware that what follows will not be particularly comprehensible without at least a cursory background of calculus. More importantly, the final result will also seem much less interesting, and we wish to avoid undue disappointment. This is by no means a warning against reading it, rather an assurance that a specific audience will appreciate it more directly.
Earlier, in showing the harmonic series H to be divergent to infinity, a rearrangement of H yielded itself plus the following extra expression S∞:
S∞ =
These were the pieces remaining when subtracting the even unit fractions from the odds. The pattern is difficult to see at a glance when written that way; if you were wondering, it is easier to notice like this:
S∞ =
However, neither of those are quite as useful as going all the way back to writing it in terms of the original differences between the odd and even unit fractions. We can also decouple those pairs, leaving an alternating version of the harmonic series:
S∞ =
S∞ = 1 −
This time, it should be clear that the remainder S cannot be an infinite value. The original grouping shows us that S must be greater than 0, and if we stagger the grouping by one term, we can see that S must be less than 1. With the terms also reducing to arbitrarily small size, this should ensure that it settles upon some single finite value.
As a matter of general practice for anyone with knowledge of calculus, seeing that pattern of denominators should always prompt your curiosity into asking whether it could be the result of polynomial integration. Constant offset permitting, we know that:
With that in mind, try reinventing S∞ as a function S∞(x) of some variable x, chosen specifically to fit that model:
S∞(x) = x −
Note that S∞(0) = 0, and that S∞(1) recovers the needed result by means of all 1n equalling 1. Despite the complicated appearance, this is actually a very valuable generalisation, because it now has a pleasant derivative with respect to x:
S∞'(x) =
This is a geometric series with factors of −x, for which we can obtain a finite remainder as before:
S∞'(x) + x S∞'(x) = 1
S'(x) =
Return to S(x) via integration, observing that the result is consistent with S∞(0) = 0:
S(x) =
Indeed, we have S(0) = ln 1 = 0, so no constant offset is required.
Our alternating harmonic series is then S(1) = ln 2, which is approximately 0.6931.
As an aside, applying the same procedure to the harmonic series H yields −ln (1 − x), which does indeed escape to (positive!) infinity as x approaches 1. We hesitate to suppose that there exists a reader for whom this is the convincing proof that H is infinite, as opposed to the more fundamental arguments earlier.
Appendix C
Recall a journey J which uses the odd harmonic method:
J = 1 +
Another way of showing that this has no limit is to use incrementally larger groupings and compare those group totals to the terms of the harmonic series H, already known to be infinite.
Begin by observing that a pair of different unit fractions will sum to more than twice the fraction at their harmonic mid-point, also known as the harmonic mean. For example, if we choose
The left side is
In general, if a unit fraction is
This is understood easily by evaluating the left side and introducing the unit factor
The numerators 2x match, so clearly this is true because the left side has a denominator which is m2 lower.
With that in mind, group our terms of J more sanely by incrementing the group size rather than doubling it, and make an elegant connection to the harmonic series H by choosing a comparison series C like this:
| n : | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | ... |
| Jn : | 1 | ... | |||||||||
| Cn : | 1 | ... |
Note that each group contains terms of C which sum together to produce a term of H.
That is, if a term of H is
Of course, we no longer have Jn > Cn universally, however we still succeed if the grouped sums within J are superior to those of C—which they are:
- By selecting paired terms from the start and end of each group and working inwards, J yields pairs of unit fractions and C yields twice their harmonic mean, thus the J-pairs must exceed the C-pairs.
- Odd groups contain a spare term in the middle, but this is always equal between J and C.
For example, to illustrate the fourth and fifth groups:
- The pairs
1 /13 1 /19 1 /15 1 /17 2 /16 4 /16 - The pairs
1 /21 1 /29 1 /23 1 /27 2 /25 1 /25 5 /25
Correspond each of those groups with a term of the harmonic series—known to be infinite, of course—and we conclude that the odd unit fraction series also grows infinitely.