Introduction

On most occasions, a topic of study at INIV begins with a question. We find that many Commanders excel at asking basic, powerful questions which have interesting answers and some enlightening knowledge to be gained.

This is not one of said occasions—or at least, not one which carried any major question to be answered or problem to be solved. It started as a minor casual observation, and became an automated system for making a selection from a set of discrete numbers such that an exact total is achieved. That is to say, for cases where the total, set and selection are all far too large to find a solution manually.

No technical achievement has ever really needed some pesky practical application to act as a sponsor, so I will proceed with what happened and what it accomplished.

Observation

As many bounty-hunting Commanders discover, using a Kill Warrant Scanner will stack up bounty claims for dozens of foreign factions. With just one or two star systems—even in close proximity—the ever-changing influence of factions across the Galaxy will ensure that the spheres of activity around those systems will capture fresh claim entries over time.

The Transactions list, being grouped by issuing faction, can reach a hundred entries this way quite easily—not that its interface was designed for reporting more than two-digit counts.

It was mid-3307 when CMDR. Aleks Zuno embarked on something of a tour, ended up with over 500 entries, then found that the Pilots' Federation claim redemption was unable to process them all in bulk. Aleksandra's displeasure at having to file hundreds of claims individually was considerable, though we pointed out that it at least presented an interesting opportunity to find the actual threshold below which the bulk-claim does work properly.

This worked quite well. The comms went silent, normal business resumed, then eventually the answer arrived:

"Two hundred and fifty-six. It failed with 257 but succeeded with 256."

Interesting indeed, 256 being exactly 2⁸. After well over a thousand years of digital electronics, humans are still producing technology which is prone to power-of-2 limitations. In any case—now we know to watch the claim counter, we know the specific limit, and that seemed to be the end of it.

That is, until Aleksandra returned a month later with over 500 claims again.

Mitigation

Aside from instituting a temporary report to track the claim entry total and train a habitual visit to Interstellar Factors, we needed a new diversion for the immediate situation. Rather than being an inconvenient means to an end, what if we could decorate that process to become an attraction of its own? What can one do when in possession of hundreds of small claims which cannot be done with a single consolidated sum?

Simple! One can opt not to claim them, or at least not claim all of them. With so many different individual quantities, the small claims at Interstellar Factors can be processed selectively, designed so that they augment the primary payouts from the controlling factions in a way which matches any nearby total of choice.

Probably. Obviously not if they all share a common factor such as 10, but they don't.

Even a Power bonus of 100% does not impose a common factor of 2, because applying the 1/4 commission for foreign claims results in a combined scale factor of 3/2. Surely the payouts from the Kill Warrant Scanner contain enough variance and few enough patterns that the amount of unique combinations increases exponentially as more entries are added, so surely just a few dozen should be enough such that any manipulation of the total becomes possible.

Sounds good, especially the part where a particularly enthusiastic huntress only has to endure the processing of a few of those entries at a time. However, what art gallery would curate this particular arithmetic¹ sculpture?

Well...

1. The adjective (as with arithmetic series), though I suppose the noun (as with modular arithmetic) also has the appropriate effect.

Presentation

INIV is an egregious consumer of data—almost anything we can acquire, whether for estimation or for inference, and motivated by anything from important efficiency optimisations to arbitrary casual interest. Scientific conditions are preferable of course, but ultimately anything is admissible as long as the analysis is honest with respect to the data quality and any sampling bias.

To that end, enter the Hutton Orbital Truckers Co-Operative, an independent faction which headquarters itself in one of the least-accessible outposts¹ in the Galaxy and keeps several substantial Sol-adjacent star systems out of Federation hands.

Quite aside from that, HOTC also maintains a regular activity report provided by CMDR. EntariusFusion and his team with the Hutton Helper, should Commanders opt to participate. As best as we can determine, it appears to be a platform intended for demonstrating quantitatively what achievements are possible, which can be a brilliant mechanism for discovering improvements to the benefit of every Commander.

Purpose aside, it serves as a public store of statistical data aggregated weekly, with which we have supported the occasional conclusion since around 3305.

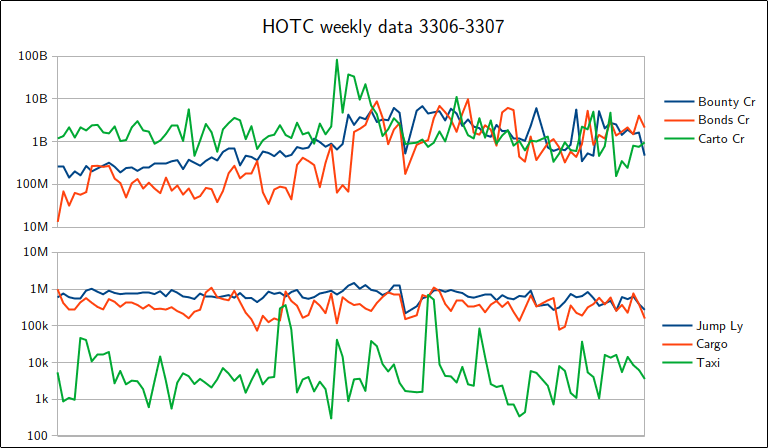
All we need here is that the total claim magnitude tops the weekly numbers, which a month² of bounty-hunting certainly does, reaching well over four billion credits. Given a claim collection large enough to top the list and the ability to apply design to the summation, and absent any infrastructure failure or administrative changes, it follows that said design will be broadcast over GalNet.

Even better, what about making the entire number interesting across the full place value range of its digits? Normally these are announced in increments of millions, so that an exact 4½ billion will just become a less interesting "four thousand, five hundred". With just a slight adjustment, we can inspire them to deviate from that format and announce every last credit.

A decent plan, if the design aspect can be achieved. Just before we have at it, first let us avoid a computational embarrassment by ensuring that the chance of being able to control the result is indeed in our favour.

1. Typically, reaching Hutton Orbital requires an entire tonne of hydrogen fuel just to maintain Supercruise (this provides 83 ⅓ minutes, where the present fastest time is 82 ⅓ minutes). If we include the other starship modules (primarily Thrusters) and the fuel cost of jumping to Alpha Centauri, this places a stock Sidewinder dangerously close to being unable to complete the journey. Many newer pilots then activate Supercruise Assist and take a nap, unaware that SCA throttles for optimum acceleration rather than maximum speed, thus eliminating completely that modest chance of success.

2. Actually, by INIV standards it is enough to reserve approximately three hours for combat, though please interpret this purely as a matter-of-fact numeric observation—the Truckers are very dedicated pilots and we are quite sure that the pace of which they are capable is just as fast, should they choose to focus on that.

Feasibility

First, let us establish the typical value of claims at Interstellar Factors with the appropriate Power bonus. INIV has plenty of this type of data; for example, consider a sample of over 700 claims, grouped into size categories every 100k credits.

Individual claims appear to average 300k credits each, mostly in a primary bell-curve between 100k and 500k credits. As an interesting statistical point, we can see smaller harmonic echoes of that base distribution, positioned at 2×, 3× and 4× the original average. Recalling that the claims are combined by faction, this should be expected! They represent factions for which two or more bounty claims have been combined.

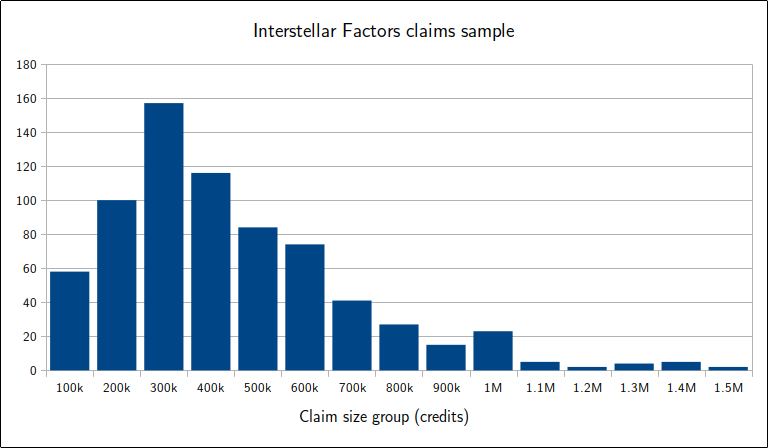
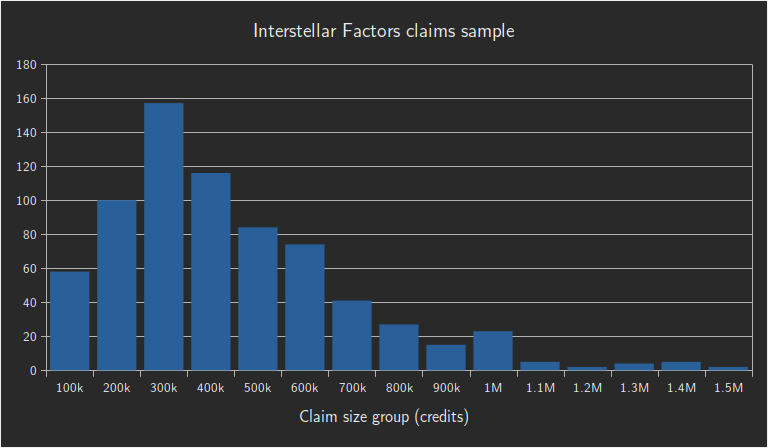
Despite the individual bounty values averaging 300k credits each, those combined claims are an unavoidable feature of this process, so we have to incorporate the fact that they raise the average entry value to 400k. This value is needed because we want to discover whether the number of claim combinations can overwhelm the range of possible totals, and knowing the average value enables us to estimate the maximum total.

To understand the number of combinations, imagine each available claim entry as being like a switch with two options: claim it or ignore it. This means that each available claim gives us a doubling¹ of combinations; for example, a set of 10 claims yields up to 2¹⁰ = 1024 combinations. Unfortunately, those 1024 combinations are distributed across a range of up to 10 × 400k = 4M credits, which leaves us with vast gaps where we cannot contrive a solution.

As you may have noticed, the range of credits is proportional but the number of combinations is exponential, so surely all we need is a larger selection of claims to make the exponential number win. How much larger, though? If n is the number of claims, we can discover that by taking a visual look at 400k·n versus 2ⁿ, with my apologies in advance to anyone familiar with data analysis.

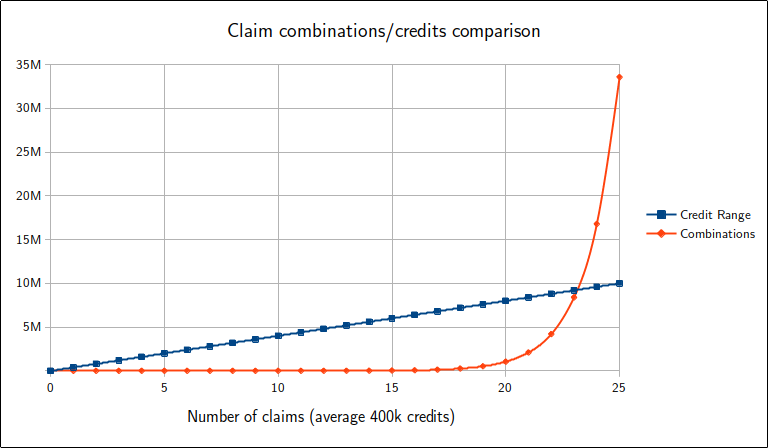
This will be the only time I draw exponential data onto a linear axis, I promise. I did it to emphasise how dramatically the number of combinations accelerates past the credits range, where that cross-over occurs at just over 23 claims. This does not mean that 24 claims are sufficient for achieving results within around 10 million credits because there will still be collisions and therefore gaps in coverage, although it marks the turning point as far as probability is concerned.

Moreover, it is clear that we can just include more and more claims to double and redouble the combinations in a way which belittles the credits range rapidly. If we model each combination result as a random number distributed uniformly² across the range, we can find an average probability of at least one combination matching some choice of target. This probability is considered best as the reverse of all combinations missing the target.

For a number of claims n with average size 400k credits, start with the chance for just one of those 2ⁿ combinations to miss the target. This is the same as hitting anything except one of those 400k·n in particular:

P(one miss) = 400k·n − 1/400k·n = 1 − 1/400k·n

Repeat that target-missed expression 2ⁿ times, then reverse it to obtain at least one hit:

P(a hit) = 1 − P(all miss) = 1 − (1 − 1/400k·n)²ⁿ

As before, view it for different n:

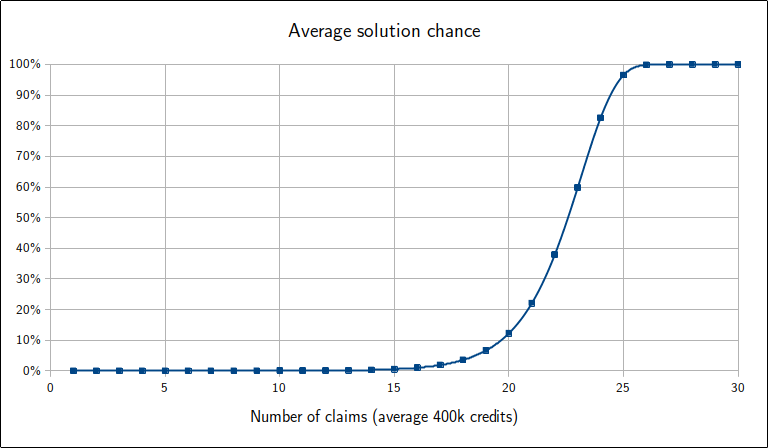
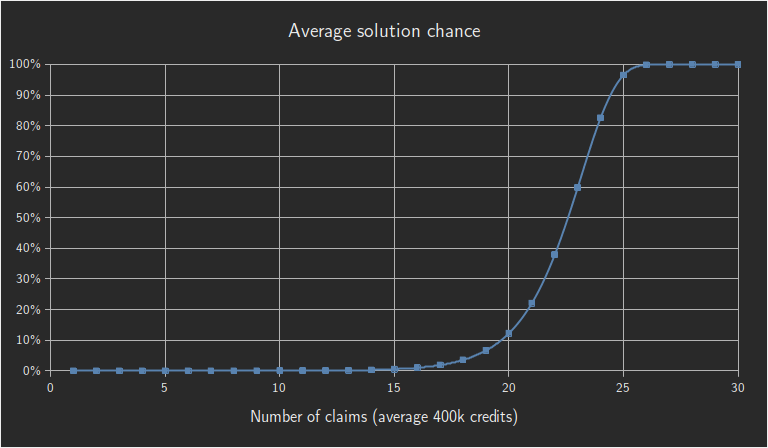
Clearly, just a few claims more than that cross-over point of 23 affords us an extreme surplus of combinations over the relatively small credits range³, all but assuring we can hit any target we choose. This result is just an average, where our combination choices are still limited at the far ends of the possible range, although this also means the probability is enhanced for targets around the middle of the range.

This is good for us; there will always be an imperceptibly tiny chance that some set of claims actually exhibits a gap where our target is set, but we can remedy that very quickly just by including one more claim, or by destroying one more pirate vessel to alter one of the existing claim values. Either of those will have the effect of introducing a new set of combinations, again with an overwhelming chance of including our target.

1. Almost. Repeat numbers can occur in the claim set, the effect of which is to upgrade the previous double to a triple (or triple to quadruple, and so on) rather than to introduce a new doubling. Also, if any single claim were to equal the sum of two other claims then this trio would represent ×7 rather than ×8. However, these are relatively rare cases, and our set of combinations becomes so vast that it matters little.

2. The actual distribution is definitely not uniform. Technically this is a binomial distribution, however we have a large enough set of switches that it becomes a near-perfect match for the classic bell-curve, called the normal distribution. With only a few special exceptions, almost all distributions become an approximate normal distribution when summed together that way, an effect known as the central limit theorem.

3. This is an excessive application of something called the pigeon-hole principle. For an absolutely astounding view of how communication and administration was implemented long ago into our ancient history on Earth, try discovering for yourself the origins of that phrase.

Implementation

As nice as it sounds to have 2ⁿ combinations available for manipulating the total, it should be no surprise that an actual search for a particular total becomes quite a difficult task, which definitely will need automation. In general, I find that the best approach here is just to get started with some form of automated search even if it would take a long time to complete, then improve it from there as needed.

Incremental search

Consider how computers implement counting and arithmetic. It is actually just a simple place-value system with factors of two rather than ten, although try looking at each column individually if you have trouble seeing the pattern.

Count		8	4	2	1
1	←				+
2	←			+
3	←			+	+
4	←		+
5	←		+		+
6	←		+	+
7	←		+	+	+
8	←	+
9	←	+			+
10	←	+		+
11	←	+		+	+
12	←	+	+
13	←	+	+		+
14	←	+	+	+
15	←	+	+	+	+

In that application, each row of bits represents a number in sequence, by means of including or excluding the value at the top of each column. Of course, those values follow a simple doubling pattern to ensure that summations of them can be used to represent any number required, a counting system named binary.

We can hijack this idea—increment the counter as with binary, but then suppose the row of bits actually encodes one of our switch combinations instead. We can just replace the doubling pattern with a list of the claim values, such that the effect of counting upwards will be to iterate through the combinations, an application known as a bitmask.

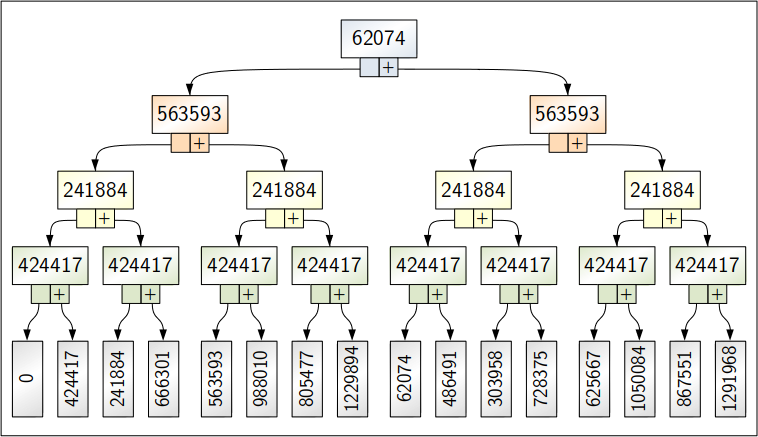
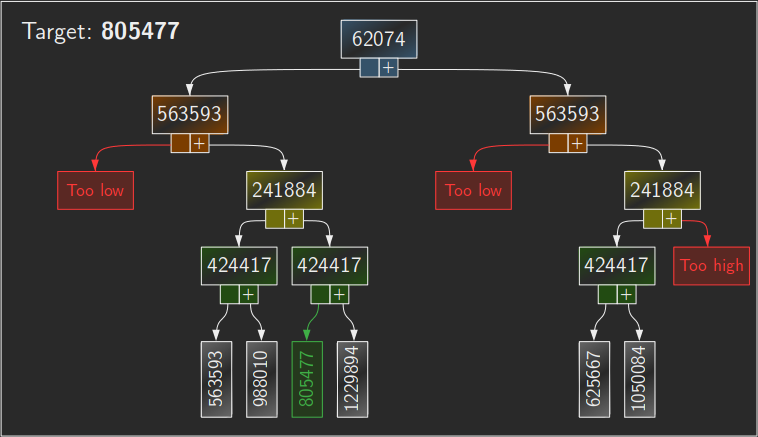
To work with an example¹, suppose we have the four claim entries 62074, 563593, 241884 and 424417:

Total		62074	563593	241884	424417
424417	←				+
241884	←			+
666301	←			+	+
563593	←		+
988010	←		+		+
805477	←		+	+
1229894	←		+	+	+
62074	←	+
486491	←	+			+
303958	←	+		+
728375	←	+		+	+
625667	←	+	+
1050084	←	+	+		+
867551	←	+	+	+
1291968	←	+	+	+	+

Certainly this will enumerate all possibilities and find a solution—eventually. In practice, I found that if an incremental search does not acquire a match within a few seconds, it will take hours to wander through billions of combinations which are nowhere near the target.

1. A small excerpt taken from Interstellar Factors, actually part of the same sample data shown earlier as a histogram. I considered dividing them by 1000 for presentation purposes, but decided it was better to remain consistent and retain authentic numbers. Hopefully it conveys both the fast expansion of possible totals from just a few claim entries, and also the need for enough claims to close the gaps in between.

Enhanced starting point

In response to that, it occurred to me that I can begin the search process with some of the switches already activated, with the effect of placing the initial total closer to the target. This need not affect the incrementing counter directly; we can just let it run as before, but consider some of the switches to be inverted as a separate operation.

Count		8	4	2	1
1	→				+
	Inv.		●	●	●
805477	←		+	+
Total		62074	563593	241884	424417

The inversions can be chosen quickly, just to make the starting point approximately close to the target. Even better, if we do that by inverting alternate switches, the search should have the effect of testing a lot of values which surround that initial number.

This had some success for particular starts more so than others, but nothing decisive in terms of a scheme which always works well. Mostly, it would test a few combinations which are close to the target, then revert to the previous case of wandering off-target for a long time.

Random starting point

Insofar as the previous idea felt as if I was guessing at random, I noticed that I could just embrace it and instruct the computer to do exactly that. With a random starting point by design, I could just keep relaunching the search if any given attempt takes longer than a few seconds, or start dozens of searches simultaneously.

Amazingly, this actually started to work. It was by no means consistent, however I could now stay with a fixed target and expect that at least some search attempts would find a result within around 10 seconds, aborting and restarting as needed.

To be honest, this relative travesty of a process was at least now above the threshold for viability. However, excellence is the standard, so I wanted improvements.

Random switching

Given that the intentional random element was somewhat successful, I took it one step further—scrap the incremental counter, and just flip switches at random.

In computing terms, this is what one might consider to be a illegitimate path, because such a process no longer qualifies as being an algorithm. One critical property of algorithms is that they finish in finite time, whereas this fully-random version has the potential to continue forever even if a solution does exist.

Of course, let that matter not diminish the fact that this worked even more successfully. A single attempt would now stumble upon a solution within around 10 seconds, usually between 5 and 15 seconds.

As erratic as it may sound, note that the search process has gained a new property which bestows one particular advantage not present with the incremental variants: flipping only one switch per check. Look again at how the previous counter increments worked, in more detail this time:

Total		62074	563593	241884	424417
424417	←				+
	Flip			●	●
241884	←			+
	Flip				●
666301	←			+	+
	Flip		●	●	●
563593	←		+

Multiple bits can change when incrementing a counter, thus requiring extra work to recompute the new total, whereas flipping a single switch demands only a single addition or subtraction. If we can modify it to use a systematic search which has that single-switch-and-check property, it could return to being a proper algorithm again.

The Gray code

Conveniently, a method already exists for doing exactly that. Rather than counting in binary directly, we could implement a Gray code¹ counter, which increments via single bit-flips by design. There are many applications for counting that way, such as reducing the electrical noise/interference in low-level hardware implementations of it, however we need it simply because there is an undesirable time expense associated with flipping multiple bits.

Here is the bitmask example again, but observe how it has been reordered so that only one column differs between any consecutive pair of rows. With only one operation to change the sum and one more to check the total, this should provide a faster version of the incremental search.

Total		62074	563593	241884	424417
424417	←				+
666301	←			+	+
241884	←			+
805477	←		+	+
1229894	←		+	+	+
988010	←		+		+
563593	←		+
625667	←	+	+
1050084	←	+	+		+
1291968	←	+	+	+	+
867551	←	+	+	+
303958	←	+		+
728375	←	+		+	+
486491	←	+			+
62074	←	+

Unfortunately, despite searching with the increased rate as was enjoyed by the random method, the sequential aspect still performed far more poorly than with random switching. Clearly, the act of stepping through each combination systematically is just not a good enough strategy if it can get stuck within a massive region of combinations where there is no hope of finding a match.

That said, it was far from a wasted effort to implement a Gray code, because the search algorithm has now gained another new property we can use. The fundamental advantage of random guesses was that they were quick to escape from hopeless regions of the search space, so any meaningful strategy needs to have that same ability, and we now have a way to achieve exactly that.

1. Yet another product of ancient Earth, named after its inventor. The history of humanity on Earth and the breadth of its legacy are popular topics within the Empire, despite the destruction of almost all original works.

Recursive walk

From the ground up, the Gray code implementation works like this:

• First stage: Flip the first switch.
• Additional stages: Flip the next switch, then do all of the previous things again.

This seems like it would involve an ever-growing mess of instructions to remember as more switches are added, which is true if implemented that way literally. However, it can also be written for an equivalent top-down approach, where each stage looks like this:

• Do all sub-stages starting at the next switch.
• Flip this switch.
• Do all sub-stages again.

This implementation is recursive, where it invokes itself in layers as a means of stepping through the set of switches, limited at the end of the line where no "next switch" exists (thus no operations to perform).

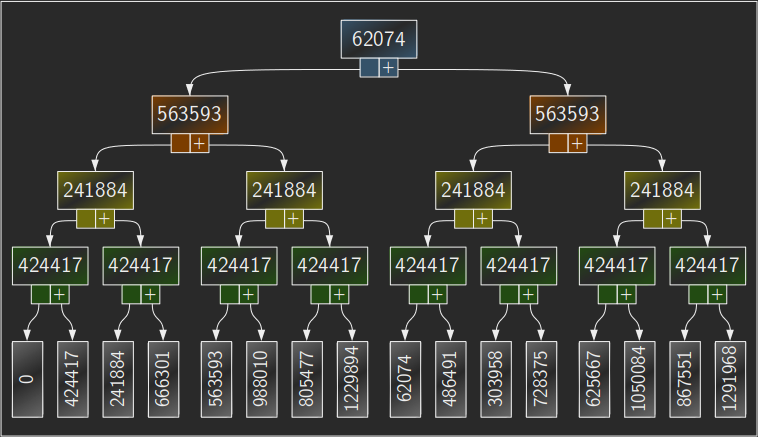
To use the first stage as an example, it is doing the following:

• Run all combinations of switches 2 through n.
• Flip switch 1.
• Run all combinations of switches 2 through n again.

Critically, notice how that first stage has exclusive control of switch 1. Its first recursion runs with switch 1 always off, which implies that all combinations therein have a lowered maximum possible total. Similarly, its second recursion runs with switch 1 always on, implying a raised minimum possible total.

The optimisation here is simple: track those extrema at each stage. At any point, if the minimum and maximum boundaries become too narrow so as not to contain the target value¹, just skip that entire recursion. For example, there is no need to test the remaining 80 of 100 switches when the first 20 have already ensured that the target cannot possibly be matched, so we can just close that path and test a different switch selection earlier in the process.

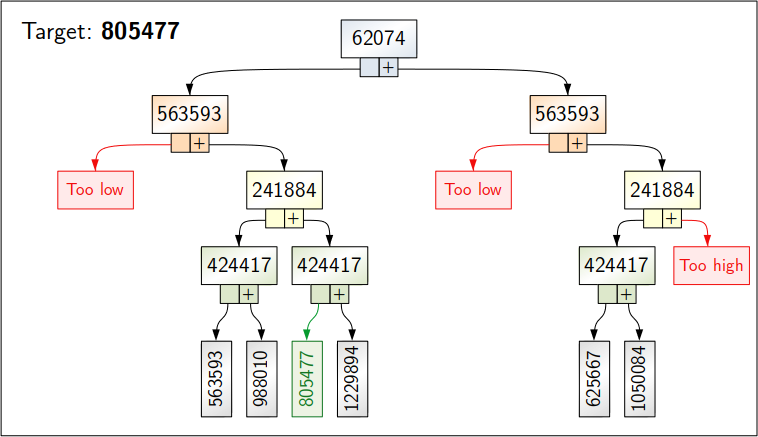
This boundary check is the true hero of the story. With that in place, the Gray code algorithm now gives a result almost immediately, every time. The astounding efficacy of that approach gave me a much-needed moment of appreciation for elegance. Most technology in the Galaxy makes me cringe; this made me smile.

All it required after that was a minor change to start the recursion process from the back of the list. This was purely for convenience at Interstellar Factors, where it is easier to have most of the selected claims biased towards the front.

Unfortunately, one still needs to transcribe dozens of claim entries. We tried to automate most of this by using optical recognition with pre-processed images of the list, however we always saw a ~1% chance of error². Exactness is important here, so we had to verify that output independently, eroding the usefulness of that idea. Entering the values manually³ is a much cheaper solution.

1. Applied strictly, this exclusion check works just fine when one is concerned only with exact matches, though it also makes the algorithm unable to track the near-miss results when no match is available. For a more intuitive user experience, it is good to allow a recursion path to proceed if it still has improvement potential, despite having no match potential.

2. A further ~1% were missing, but the errors are the critical problem.

3. Ideally we would be able to obtain the list data electronically, but working with the Pilots' Federation here is expensive, and we judge technology against purchasing labour to achieve the same effect. Under that benchmark, we prevent bad technology from prevailing, because Imperial labour is very cheap.

Result

The investment was a heavily-armed Mamba starship engineered to perfection, a month of stacking bounty claims skilfully and carefully, an adventurous idea for what to do with them, and non-trivial effort towards designing and deploying a solution. Minor, in comparison to its yield of interesting discoveries along the way.

Not to mention...

No material prize in the Galaxy can replace that.

● ● ●

Given a present total, target total and claim entries available, the following GalNet adaptation of our original system should be capable of identifying a match, or a close result if no match exists. Feel free to use it yourself.

Remember that these should be only your Interstellar Factors claims, not the primary claim payload from local factions. You will need the combined total to approach your required number carefully. For a decent approximation:

• Stop when the sum at a foreign ISF (or a Fleet Carrier) reaches 80% of your target¹.
• Redeem the local claims locally, keeping track of that initial total.
• Use the solver below to redeem the difference at ISF.

To demonstrate how it works, load an example case then press Solve. Go ahead and change the target, or delete some of the entries it attempted to use. It will find another way.

A page with only the solver is also available for convenience.

1. This is because the local to foreign ratio is approximately 3:1. Relative to ISF, redeeming the local claims locally makes them worth 4:1, so if these 5 parts should equal 100% then the original measurement of 4 parts needs to be 80%.